Generation of Legendre polynomials

In order to perform the Legendre polynomials, ecTrans precomputes and stores the associated Legendre polynomials. Following convention, this is done using a recurrence relation. In fact, we use several recurrence relations depending on the mode of the polynomial which is being generated, refined over several decades of experience.

Here we summarise in mathematical notation the recurrence formulae followed by the relevant subroutine, SUPOLF. This subroutine takes in a zonal wavenumber and a single abscissa (i.e. a single value of the sine of latitude) and returns an array corresponding to the associated Legendre polynomial values for all total wavenumbers valid for that zonal wavenumber evaluated at the given abscissa coordinate. As always, a triangular truncation is used, such that the highest total wavenumber that a polynomial is evaluated at is the same as the zonal wavenumber truncation.

Now we describe how the polynomial array, $P_{m,n}(\mu)$ is filled, where $m$ is the zonal wavenumber, $n$ is the total wavenumber, and $\mu$ is the sine of the latitude. The recurrence relation used is different depending on $m$.

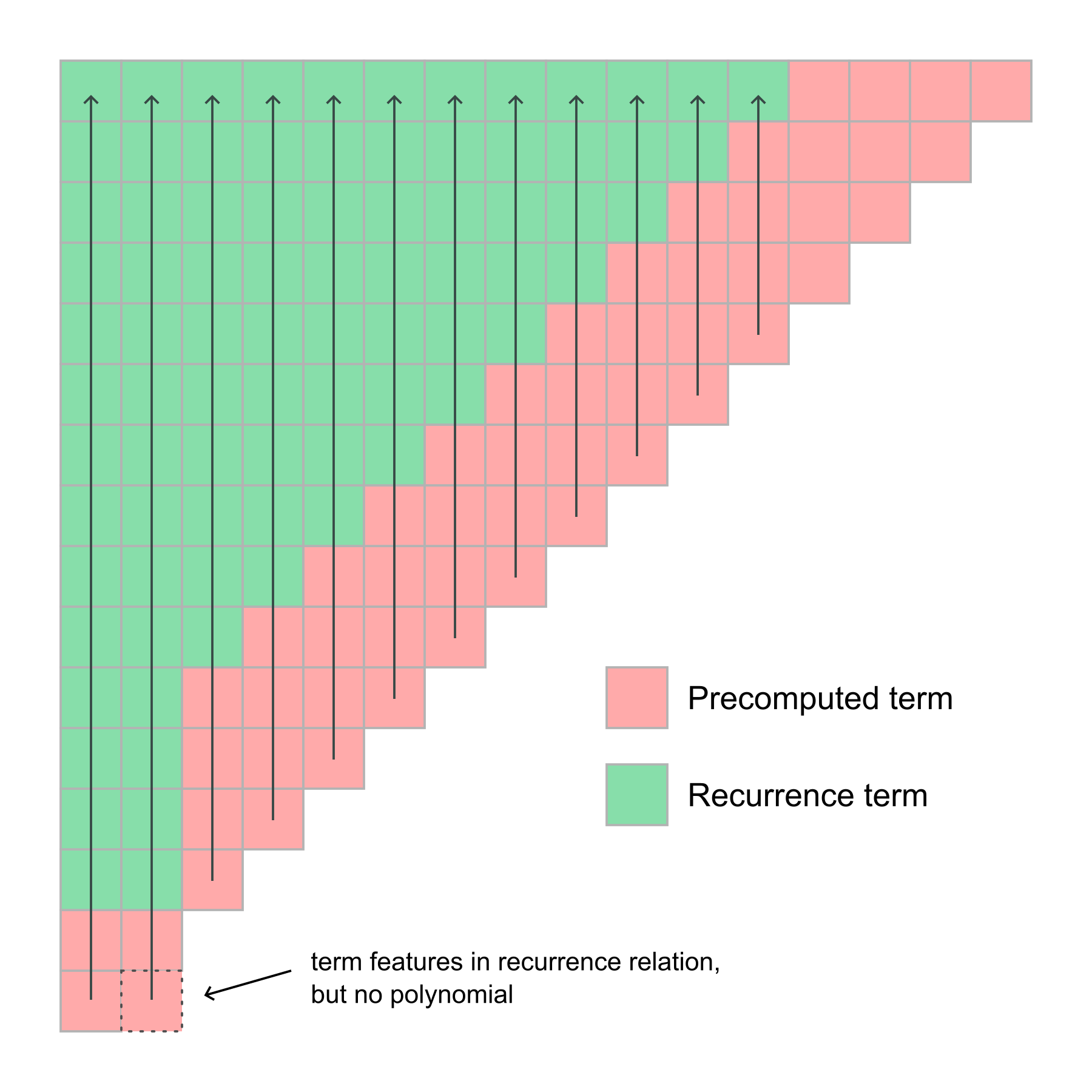
$m = 0$ case

$$\begin{align*} d_0 &= 1, &P_{0,0}(\mu) = d_0\\ d_1 &= \mu, &P_{0,1}(\mu) = \sqrt{3}d_1\\ d_n &= \frac{2n-1}{n}\mu d_{n-1} - \frac{n-1}{n}d_{n-2}, &P_{0,n}(\mu) = d_n\sqrt{2n+1} \end{align*}$$

$m = 1$ case

$$\begin{align*} d_0 &= 1\\ d_1 &= \mu, &P_{1,1}(\mu) = \sqrt{\frac{3}{2}(1 - \mu^2)}\\ d_n &= \frac{2n-1}{n}\mu d_{n-1} - \frac{n-1}{n}d_{n-2}, &P_{1,n}(\mu) = n\frac{(d_{n-1} - \mu d_n)}{\sqrt{1-\mu^2}}\sqrt{\frac{2n+1}{n(n+1)}} \end{align*}$$